Coordinate System

The three mutually perpendicular lines in a space which divides the space into eight parts and if these perpendicular lines are the coordinate axes, then it is said to be a coordinate system.

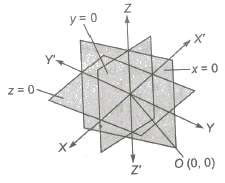
Sign Convention

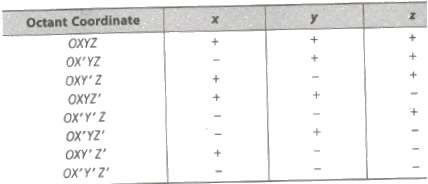
Distance between Two Points

Let P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) be two given points. The distance between these points is given by PQ √(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²

The distance of a point P(x, y, z) from origin O is OP = √x² + y² + z²

Section Formulae

(i) The coordinates of any point, which divides the join of points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) in the ratio m : n internally are (mx₂ + nx₁ / m + n, my₂ + ny₁ / m + n, mz₂ + nz₁ / m + n)
(ii) The coordinates of any point, which divides the join of points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) in the ratio m : n externally are (mx₂ – nx₁ / m – n, my₂ – ny₁ / m – n, mz₂ – nz₁ / m – n)
(iii) The coordinates of mid-point of P and Q are (x₁ + x₂ / 2 , y₁ + y₂ / 2, z₁ + z₂ / 2)
(iv) Coordinates of the centroid of a triangle formed with vertices P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) and R(x₃, y₃, z₃) are (x₁ + x₂ + x₃ / 3 , y₁ + y₂ + y₃ / 3, z₁ + z₂ + z₃ / 3)
(v) Centroid of a Tetrahedron
If (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃) and (x₄, y₄, z₄) are the vertices of a tetrahedron, then its centroid G is given by (x₁ + x₂ + x₃ + x₄ / 4 , y₁ + y₂ + y₃ + y₄ / 4, z₁ + z₂ + z₃ + z₄ / 4)

Direction Cosines

If a directed line segment OP makes angle α, β and γ with OX , OY and OZ respectively, then Cos α, cos β and cos γ are called direction cosines of up and it is represented by l, m, n.
i.e.,
l = cos α
m = cos β and n = cos γ

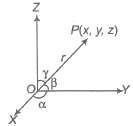
If OP = r, then coordinates of OP are (lr, mr , nr)

(i) If 1, m, n are direction cosines of a vector r, then
(a) r = |r| (li + mj + nk) ⇒ r = li + mj + nk
(b) l² + m² + n² = 1
(c) Projections of r on the coordinate axes are
(d) |r| = l|r|, m|r|, n|r| / √sum of the squares of projections of r on the coordinate axes

(ii) If P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) are two points, such that the direction cosines of PQ are l, m, n. Then, x₂ – x₁ = l|PQ|, y₂ – y₁ = m|PQ|, z₂ – z₁ = n|PQ| These are projections of PQ on X , Y and Z axes, respectively.
(iii) If 1, m, n are direction cosines of a vector r and a b, c are three numbers, such that l / a = m / b = n / c.
Then, we say that the direction ratio of r are proportional to a, b, Also, we have l = a / √a₂ + b₂ + c₂, m = b / √a₂ + b₂ + c₂, n = c / √a₂ + b₂ + c₂
(iv) If θ is the angle between two lines having direction cosines l₁, m₁, n₁ and 1₂, m₂, n₂, then cos θ = l₁1₂ + m₁m₂ + n₁n₂
(a) Lines are parallel, if l₁ / 1₂ = m₁ / m₂ = n₁ / n₂
(b) Lines are perpendicular, if l₁1₂ + m₁m₂ + n₁n₂
(v) If θ is the angle between two lines whose direction ratios are proportional to a₁, b₁, c₁ and a₂, b₂, c₂ respectively, then the angle θ between them is given by cos θ = a₁a₂ + b₁b₂ + c₁c₂ / √a² ₁ + b² ₁ + c² ₁ √a² ₂ + b² ₂ + c² ₂
Lines are parallel, if a₁ / a₂ = b₁ / b2 = c₁ / c2
Lines are perpendicular, if a₁a2 + b₁b₂ + c₁c₂ = 0.
(vi) The projection of the line segment joining points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) to the line having direction cosines 1, m, n is |(x₂ – x₁)l + (y₂ – y₁)m + (z₂ – z₁)n|.
(vii) The direction ratio of the line passing through points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) are proportional to x₂ – x₁, y₂ – y₁ – z₂ – z₁
Then, direction cosines of PQ arex₂ – x₁ / |PQ|, y₂ – y₁ / |PQ|, z₂ – z₁ / |PQ|

Area of Triangle

If the vertices of a triangle be A(x₁, y₁, z₁) and B(x₂, y₂, z₂) and C(x₃, y₃, z₃), then

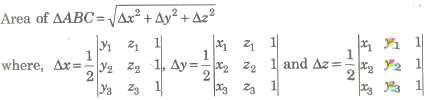
Angle Between Two Intersecting Lines

If l(x₁, m₁, n₁) and l(x₂, m₂, n₂) be the direction cosines of two given lines, then the angle θ between them is given by cos θ = l₁1₂ + m₁m₂ + n₁n₂

(i) The angle between any two diagonals of a cube is cos-1 (1 / 3).
(ii) The angle between a diagonal of a cube and the diagonal of a face (of the cube is cos-1 (√2 / 3)

Straight Line in Space

The two equations of the line ax + by + cz + d = 0 and a’ x + b’ y + c’ z + d’ = 0 together represents a straight line.

1. Equation of a straight line passing through a fixed point A(x₁, y₁, z₁) and having direction ratios a, b, c is given by x – x₁ / a = y – y₁ / b = z – z₁ / c, it is also called the symmetrically form of a line.
Any point P on this line may be taken as (x₁ + λa, y₁ + λb, z₁ + λc), where λ ∈ R is parameter. If a, b, c are replaced by direction cosines 1, m, n, then λ, represents
distance of the point P from the fixed point A.

 

2. Equation of a straight line joining two fixed points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) is given by x – x₁ / x₂ – x₁ = y – y₁ / y₂ – y₁ = z – z₁ / z₂ – z₁

3. Vector equation of a line passing through a point with position vector a and parallel to vector b is r = a + λ b, where A, is a parameter.

4. Vector equation of a line passing through two given points having position vectors a and b is r = a + λ (b – a) , where λ is a parameter.

5. (a) The length of the perpendicular from a point on the line r – a + λ b is given by

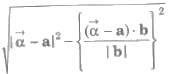
(b) The length of the perpendicular from a point P(x₁, y₁, z₁) on the line

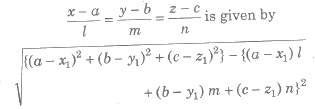
where, 1, m, n are direction cosines of the line.

6. Skew Lines Two straight lines in space are said to be skew lines, if they are neither parallel
nor intersecting.

7. Shortest Distance If l₁ and l₂ are two skew lines, then a line perpendicular to each of lines 4 and 12 is known as the line of shortest distance.

If the line of shortest distance intersects the lines l₁ and l₂ at P and Q respectively, then the distance PQ between points P and Q is known as the shortest distance between l₁ and l₂.

8. The shortest distance between the lines

9. The shortest distance between lines r = a₁ + λb₁ and r = a₂ + μb₂ is given by

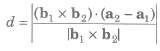
10. The shortest distance parallel lines r = a₁ + λb₁ and r = a₂ + μb₂ is given by

11. Lines r = a₁ + λb₁ and r = a₂ + μb₂ are intersecting lines, if (b₁ * b₂) * (a₂ – a₁) = 0.

12. The image or reflection (x, y, z) of a point (x₁, y₁, z₁) in a plane ax + by + cz + d = 0 is given by x – x₁ / a = y – y₁ / b = z – z₁ / c = – 2 (ax₁ + by₁ + cz1 + d) / a₂ + b₂ + c₂

13. The foot (x, y, z) of a point (x₁, y₁, z₁) in a plane ax + by + cz + d = 0 is given by x – x₁ / a = y – y₁ / b = z – z₁ / c = – (ax₁ + by₁ + cz₁ + d) / a₂ + b₂ + c₂

14. Since, x, y and z-axes pass through the origin and have direction cosines (1, 0, 0), (0, 1, 0) and (0, 0, 1), respectively. Therefore, their equations are
x – axis : x – 0 / 1 = y – 0 / 0 = z – 0 / 0
y – axis : x – 0 / 0 = y – 0 / 1 = z – 0 / 0z – axis : x – 0 / 0 = y – 0 / 0 = z – 0 / 1

 

Plane

A plane is a surface such that, if two points are taken on it, a straight line joining them lies wholly in the surface.

General Equation of the Plane

The general equation of the first degree in x, y, z always represents a plane. Hence, the general equation of the plane is ax + by + cz + d = 0. The coefficient of x, y and z in the cartesian equation of a plane are the direction ratios of normal to the plane.

Equation of the Plane Passing Through a Fixed Point

The equation of a plane passing through a given point (x₁, y₁, z₁) is given by a(x – x₁) + b (y — y₁) + c (z — z₁) = 0.

Normal Form of the Equation of Plane

(i) The equation of a plane, which is at a distance p from origin and the direction cosines of the normal from the origin to the plane are l, m, n is given by lx + my + nz = p.
(ii) The coordinates of foot of perpendicular N from the origin on the plane are (1p, mp, np).

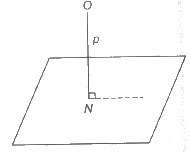
Intercept Form

The intercept form of equation of plane represented in the form of x / a + y / b + z / c = 1
where, a, b and c are intercepts on X, Y and Z-axes, respectively.
For x intercept Put y = 0, z = 0 in the equation of the plane and obtain the value of x. Similarly, we can determine for other intercepts.

Equation of Planes with Given Conditions

(i) Equation of a plane passing through the point A(x₁, y₁, z₁) and parallel to two given lines with direction ratios

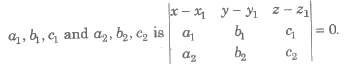
(ii) Equation of a plane through two points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) and parallel to a line with direction ratios a, b, c is

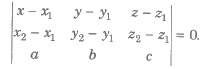
(iii) The Equation of a plane passing through three points A(x₁, y₁, z₁), B(x₂, y₂, z₂) and C(x₃, y₃, z₃) is

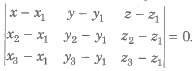
(iv) Four points A(x₁, y₁, z₁), B(x₂, y₂, z₂), C(x₃, y₃, z₃) and D(x₄, y₄, z₄) are coplanar if and only if

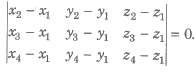
(v) Equation of the plane containing two coplanar lines

Angle between Two Planes

The angle between two planes is defined as the angle between the normal to them from any point.
Thus, the angle between the two planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0

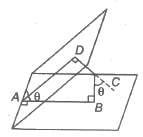
is equal to the angle between the normals with direction cosines ± a₁ / √Σ a² ₁, ± b₁ / √Σ a² ₁, ± c₁ / √Σ a² ₁ and ± a₂ / √Σ a² ₂, ± b₂ / √Σ a² ₂, ± c2 / √Σ a² ₂

If θ is the angle between the normals, then cos θ = ± a₁a₂ + b₁b₂ + c₁c₂ / √a²₁ + b² ₁ + c² ₁ √a2 ₂ + b2 ₂ + c2 ₂

 

Parallelism and Perpendicularity of Two Planes

Two planes are parallel or perpendicular according as the normals to them are parallel or perpendicular.
Hence, the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 are parallel, if a₁ / a₂ = b₁ / b₂ = c₁ / c₂ and perpendicular, if a₁a₂ + b₁b₂ + c₁c₂ = 0.
Note The equation of plane parallel to a given plane ax + by + cz + d = 0 is given by ax + by + cz + k = 0, where k may be determined from given conditions.

Angle between a Line and a Plane

In Vector Form The angle between a line r = a + λ b and plane r *• n = d, is defined as the complement of the angle between the line and normal to the plane:

sin θ = n * b / |n||b|

In Cartesian Form The angle between a line x – x₁ / a₁ = y – y₁ / b₁ = z – z₁ / c₁ and plane a₂x + b₂y + c₂z + d₂ = 0 is sin θ = a₁a₂ + b₁b₂ + c₁c / √a² ₁ + b² ₁ + c² ₁ √a_²2 + b² ₂ + c² ₂

Distance of a Point from a Plane

Let the plane in the general form be ax + by + cz + d = 0. The distance of the point P(x₁, y₁, z₁) from the plane is equal to

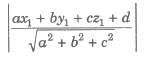
If the plane is given in, normal form lx + my + nz = p. Then, the distance of the point P(x₁, y₁, z₁) from the plane is |lx₁ + my₁ + nz₁ – p|.

Distance between Two Parallel Planes

If ax + by + cz + d1 = 0 and ax + by + cz + d₂ = 0 be equation of two parallel planes. Then, the distance between them is

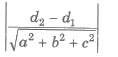
Bisectors of Angles between Two Planes

The bisector planes of the angles between the planes a₁x + b₁y + c₁z + d₁ = 0, a₂x + b₂y + c₂z + d₂ = 0 is a₁x + b₁y + c₁z + d₁ / √Σa² ₁ = ± a₂x + b₂y + c₂z + d₂ / √Σa² ₂

One of these planes will bisect the acute angle and the other obtuse angle between the given plane.

Sphere

A sphere is the locus of a point which moves in a space in such a way that its distance from a fixed point always remains constant.

General Equation of the Sphere

In Cartesian Form

The equation of the sphere with centre (a, b, c) and radius r is (x – a)² + (y – b)² + (z – c)² = r² …….(i)
In generally, we can write x² + y² + z² + 2ux + 2vy + 2wz + d = 0
Here, its centre is (-u, v, w) and radius = √u² + v² + w² – d

In Vector Form

The vector equation of a sphere of radius a and Centre having position vector c is |r – c| = a

Important Points to be Remembered

(i) The general equation of second degree in x, y, z is ax² + by² + cz² + 2hxy + 2kyz + 2lzx + 2ux + 2vy + 2wz + d = 0 represents a sphere, if
(a) a = b = c (≠ 0)
(b) h = k = 1 = 0
The equation becomes ax² + ay² + az² + 2ux + 2vy + 2wz + d – 0 …(A)

To find its centre and radius first we make the coefficients of x², y² and z² each unity by dividing throughout by a.
Thus, we have x²+y²+z² + (2u / a) x + (2v / a) y + (2w / a) z + d / a = 0 …..(B)
∴ Centre is (- u / a, – v / a, – w / a)
and radius = √u² / a² + v² / a² + w² / a² – d / a
= √u² + v² + w² – ad / |a| .

(ii) Any sphere concentric with the sphere x² + y² + z² + 2ux + 2vy + 2wz + d = 0 is x² + y² + z² + 2ux + 2vy + 2wz + k = 0
(iii) Since, r² = u² + v² + w² — d, therefore, the Eq. (B) represents a real sphere, if u² +v² + w² — d > 0
(iv) The equation of a sphere on the line joining two points (x₁, y₁, z₁) and (x₂, y₂, z₂) as a diameter is
(x – x₁) (x – x₁) + (y – y₁) (y – y₂) + (z – z₁) (z – z₂) = 0.
(v) The equation of a sphere passing through four non-coplanar points (x₁, y₁, z₁), (x₂, y₂, z₂),
(x₃, y₃, z₃) and (x₄, y₄, z₄) is

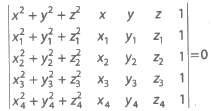
Tangency of a Plane to a Sphere

The plane lx + my + nz = p will touch the sphere x² + y² + z² + 2ux + 2vy + 2 wz + d = 0, if length of the perpendicular from the centre ( – u, – v,— w)= radius, i.e., |lu – mv – nw – p| / √l² + m² + n²
= √u² + v² + w² – d (lu – mv – nw – p)² = (u² + v² + w² – d) (l² + m² + n²)

Plane Section of a Sphere

Consider a sphere intersected by a plane. The set of points common to both sphere and plane is called a plane section of a sphere. In ΔCNP, NP² = CP² – CN² = r² – p²
∴ NP = √r² – p²

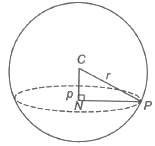
Hence, the locus of P is a circle whose centre is at the point N, the foot of the perpendicular from the centre of the sphere to the plane.
The section of sphere by a plane through its centre is called a great circle. The centre and radius of a great circle are the same as those of the sphere.