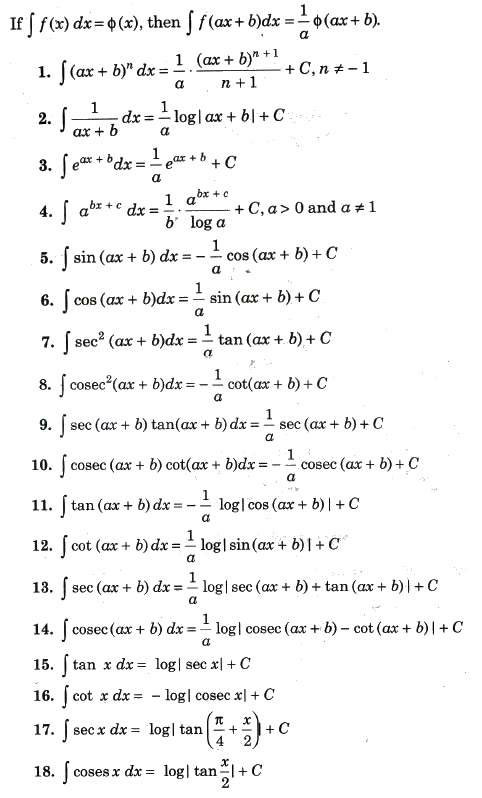-
1.Relations and Functions
11-
Revision – Functions and its Types 38 minLecture1.1
-
Revision – Functions Types 17 minLecture1.2
-
Revision – Sum Related to Relations 04 minLecture1.3
-
Revision – Sums Related to Relations, Domain and Range 22 minLecture1.4
-
Cartesian Product of Sets, Relation, Domain, Range, Inverse of Relation, Types of Relations 34 minLecture1.5
-
Functions, Intervals 39 minLecture1.6
-
Domain 01 minLecture1.7
-
Problem Based on finding Domain and Range 39 minLecture1.8
-
Types of Real function 31 minLecture1.9
-
Odd & Even Function, Composition of Function 32 minLecture1.10
-
Chapter Notes – Relations and FunctionsLecture1.11
-
-
2.Inverse Trigonometric Functions
16-
Revision – Introduction, Some Identities and Some Sums 16 minLecture2.1
-
Revision – Some Sums Related to Trigonometry Identities, trigonometry Functions Table and Its Quadrants 35 minLecture2.2
-
Revision – Trigonometrical Identities-Some important relations and Its related Sums 16 minLecture2.3
-
Revision – Sums Related to Trigonometrical Identities 18 minLecture2.4
-
Revision – Some Trigonometric Identities and its related Sums 42 minLecture2.5
-
Revision – Trigonometry Equations 44 minLecture2.6
-
Revision – Sum Based on Trigonometry Equations 08 minLecture2.7
-
Introduction to Inverse Trigonometry Function, Range, Domain, Question based on Principal Value 37 minLecture2.8
-
Property -1 of Inverse trigo function 28 minLecture2.9
-
Property -2 to 4 of Inverse trigo function 48 minLecture2.10
-
Questions based on properties of Inverse trigo function 19 minLecture2.11
-
Question based on useful substitution 27 minLecture2.12
-
Numerical problems 19 minLecture2.13
-
Numerical problems 24 minLecture2.14
-
Numerical problems , introduction to Differentiation 44 minLecture2.15
-
Chapter Notes – Inverse Trigonometric FunctionsLecture2.16
-
-
3.Matrices
9-
What is matrix 26 minLecture3.1
-
Types of matrix 28 minLecture3.2
-
Operations of matrices 28 minLecture3.3
-
Multiplication of matrices 29 minLecture3.4
-
Properties of a matrices 44 minLecture3.5
-
Numerical problems 19 minLecture3.6
-
Solution of simultaneous linear equation 28 minLecture3.7
-
Solution of simultaneous / Homogenous linear equation 24 minLecture3.8
-
Chapter Notes – MatricesLecture3.9
-
-
4.Determinants
6-
Introduction of Determinants 23 minLecture4.1
-
Properties of Determinants 29 minLecture4.2
-
Numerical problems 15 minLecture4.3
-
Numerical problems 16 minLecture4.4
-
Applications of Determinants 17 minLecture4.5
-
Chapter Notes – DeterminantsLecture4.6
-
-
5.Continuity
7-
Introduction to continuity 28 minLecture5.1
-
Numerical problems 17 minLecture5.2
-
Numerical problems 22 minLecture5.3
-
Basics of continuity 26 minLecture5.4
-
Numerical problems 17 minLecture5.5
-
Numerical problems 11 minLecture5.6
-
Chapter Notes – Continuity and DifferentiabilityLecture5.7
-
-
6.Differentiation
14-
Introduction to Differentiation 27 minLecture6.1
-
Important formula’s 29 minLecture6.2
-
Numerical problems 29 minLecture6.3
-
Numerical problems 31 minLecture6.4
-
Differentiation by using trigonometric substitution 21 minLecture6.5
-
Differentiation of implicit function 21 minLecture6.6
-
Differentiation of logarthmetic function 31 minLecture6.7
-
Differentiation of log function 25 minLecture6.8
-
Infinite series & parametric function 26 minLecture6.9
-
Infinite series & parametric function 27 minLecture6.10
-
Higher order derivatives 27 minLecture6.11
-
Differentiation of function of a function 16 minLecture6.12
-
Numerical problems 27 minLecture6.13
-
Numerical problems 04 minLecture6.14
-
-
7.Mean Value Theorem
4-
Lagrange theorem 24 minLecture7.1
-
Rolle’s theorem 20 minLecture7.2
-
Lagrange theorem 24 minLecture7.3
-
Rolle’s theorem 20 minLecture7.4
-
-
8.Applications of Derivatives
6-
Rate of change of Quantities 30 minLecture8.1
-
Rate of change of Quantities 18 minLecture8.2
-
Rate of change of Quantities 18 minLecture8.3
-
Approximation 10 minLecture8.4
-
Approximation 05 minLecture8.5
-
Chapter Notes – Applications of DerivativesLecture8.6
-
-
9.Increasing and Decreasing Function
5-
Introduction 36 minLecture9.1
-
Numerical Problem 26 minLecture9.2
-
Numerical Problem 22 minLecture9.3
-
Numerical Problem 22 minLecture9.4
-
Numerical Problem 21 minLecture9.5
-
-
10.Tangents and Normal
3-
Introduction 34 minLecture10.1
-
Numerical Problems 32 minLecture10.2
-
Angle of intersection of two curves 27 minLecture10.3
-
-
11.Maxima and Minima
10-
Introduction 28 minLecture11.1
-
Local maxima & Local Minima 27 minLecture11.2
-
Numerical Problems 37 minLecture11.3
-
Maximum & minimum value in closed interval 19 minLecture11.4
-
Application of Maxima & Minima 10 minLecture11.5
-
Application of Maxima & Minima 14 minLecture11.6
-
Numerical Problems 17 minLecture11.7
-
Numerical Problems 18 minLecture11.8
-
Numerical Problems 15 minLecture11.9
-
Numerical Problems 14 minLecture11.10
-
-
12.Integrations
19-
Introduction to Indefinite Integration 37 minLecture12.1
-
Integration by substitution 25 minLecture12.2
-
Numerical problems on Substitution 39 minLecture12.3
-
Numerical problems on Substitution 04 minLecture12.4
-
Integration various types of particular function (Identities) 31 minLecture12.5
-
Integration by parts-1 18 minLecture12.6
-
Integration by parts-2 10 minLecture12.7
-
Integration by parts-2 16 minLecture12.8
-
Integration by parts-2 08 minLecture12.9
-
ILATE Rule 12 minLecture12.10
-
Integration of some special function 07 minLecture12.11
-
Integration of some special function 06 minLecture12.12
-
Integration by substitution using trigonometric 14 minLecture12.13
-
Evaluation of some specific Integration 12 minLecture12.14
-
Evaluation of some specific Integration 29 minLecture12.15
-
Integration by partial fraction 27 minLecture12.16
-
Integration of some special function 11 minLecture12.17
-
Numerical Problems based on partial fraction 20 minLecture12.18
-
Chapter Notes – IntegralsLecture12.19
-
-
13.Definite Integrals
11-
Introduction 24 minLecture13.1
-
Properties of Definite Integration 19 minLecture13.2
-
Numerical problem based on properties 22 minLecture13.3
-
Area under the curve 16 minLecture13.4
-
Area under the curve (Ellipse) 20 minLecture13.5
-
Area under the curve (Parabola) 10 minLecture13.6
-
Area under the curve (Parabola & Circle) 40 minLecture13.7
-
Area bounded by lines 10 minLecture13.8
-
Numerical problems 25 minLecture13.9
-
Area under the curve (Circle ) 02 minLecture13.10
-
Chapter Notes – Application of IntegralsLecture13.11
-
-
14.Differential Equations
6-
Introduction to chapter 38 minLecture14.1
-
Solution of D.E. – Variable separation methods 14 minLecture14.2
-
Solution of D.E. – Variable separation methods 27 minLecture14.3
-
Solution of D.E. – Second order 21 minLecture14.4
-
Homogeneous D.E. 31 minLecture14.5
-
Chapter Notes – Differential EquationsLecture14.6
-
-
15.Vectors
12-
Introduction , Basic concepts , types of vector 34 minLecture15.1
-
Position vector, distance between two points, section formula 44 minLecture15.2
-
Numerical problem 02 minLecture15.3
-
collinearity of points and coplanarity of vector 34 minLecture15.4
-
Direction cosine 18 minLecture15.5
-
Projection , Dot product, Cauchy- Schwarz inequality 24 minLecture15.6
-
Numerical problem (dot product) 20 minLecture15.7
-
Vector (Cross) product , Lagrange’s Identity 15 minLecture15.8
-
Numerical problem (cross product) 38 minLecture15.9
-
Numerical problem (cross product) 06 minLecture15.10
-
Numerical problem (cross product) 22 minLecture15.11
-
Chapter Notes – VectorsLecture15.12
-
-
16.Three Dimensional Geometry
7-
Introduction to 3D, axis in 3D, plane in 3D, Distance between two points 32 minLecture16.1
-
Numerical problems , section formula , centroid of a triangle 35 minLecture16.2
-
projection , angle between two lines 40 minLecture16.3
-
Numerical Problem based on Direction ratio & cosine 02 minLecture16.4
-
locus of any point 15 minLecture16.5
-
Numerical Problem based on locus 16 minLecture16.6
-
Chapter Notes – Three Dimensional GeometryLecture16.7
-
-
17.Direction Cosine
2-
Introduction 34 minLecture17.1
-
Angle Between two vectors 25 minLecture17.2
-
-
18.Plane
3-
Introduction to plane , general equation of a plane , normal form 31 minLecture18.1
-
Angle between two planes 30 minLecture18.2
-
Distance of a point from a plane 29 minLecture18.3
-
-
19.Straight Lines
22-
Revision – Introduction, Equation of Line, Slope or Gradient of a line 24 minLecture19.1
-
Revision – Sums Related to Finding the Slope, Angle Between two Lines 22 minLecture19.2
-
Revision – Cases for Angle B/w two Lines, Different forms of Line Equation 23 minLecture19.3
-
Revision – Sums Related Finding the Equation of Line 27 minLecture19.4
-
Revision – Sums based on Previous Concepts of Straight line 32 minLecture19.5
-
Revision – Parametric Form of a Straight Line 16 minLecture19.6
-
Revision – Sums Related to Parametric Form of a Straight Line 17 minLecture19.7
-
Revision – Sums Based on Concurrent of lines, Angle b/w Two Lines 45 minLecture19.8
-
Revision – Different condition for Angle b/w two lines 04 minLecture19.9
-
Revision – Sums Based on Angle b/w Two Lines 36 minLecture19.10
-
Revision – Equation of Straight line Passes Through a Point and Make an Angle with Another Line 09 minLecture19.11
-
Revision – Sums Based on Equation of Straight line Passes Through a Point and Make an Angle with Another Line 15 minLecture19.12
-
Revision – Sums Based on Equation of Straight line Passes Through a Point and Make an Angle with Another Line 17 minLecture19.13
-
Revision – Finding the Distance of a point from the line 35 minLecture19.14
-
Revision – Sum Based on Finding the Distance of a point from the line and B/w Two Parallel Lines 33 minLecture19.15
-
Introduction to straight line , symmetric form , Angle between the lines 27 minLecture19.16
-
Numerical Problem 18 minLecture19.17
-
Angle between two lines 32 minLecture19.18
-
Unsymmetric form of Line 26 minLecture19.19
-
Numerical problem , perpendicular distance of a point from a line 22 minLecture19.20
-
Numerical Problem 21 minLecture19.21
-
Numerical problem , Condition for a line lie on a plane 26 minLecture19.22
-
-
20.Straight Lines (Vector)
4-
Vector and Cartesian equation of a straight line 27 minLecture20.1
-
Angle between two straight line 25 minLecture20.2
-
Numerical problems 37 minLecture20.3
-
Shortest Distance between two lines 22 minLecture20.4
-
-
21.Linear Programming
5-
Introduction to L.P. 30 minLecture21.1
-
Numerical Problems 43 minLecture21.2
-
Numerical Problems 23 minLecture21.3
-
Numerical Problems 17 minLecture21.4
-
Chapter Notes – Linear ProgrammingLecture21.5
-
-
22.Probability
23-
Introduction to probability 41 minLecture22.1
-
Types of events 42 minLecture22.2
-
Numerical problems 30 minLecture22.3
-
Conditional probability 12 minLecture22.4
-
Numerical problems 09 minLecture22.5
-
Numerical problems (conditional Probability) 04 minLecture22.6
-
Numerical problems (conditional Probability) 06 minLecture22.7
-
Numerical problems (conditional Probability) 05 minLecture22.8
-
Numerical problems (conditional Probability) 06 minLecture22.9
-
Bayes’ Theorem 17 minLecture22.10
-
Numerical problem ( conditional Probability) 04 minLecture22.11
-
Numerical problem ( Baye’s Theorem) 19 minLecture22.12
-
Numerical problem ( Baye’s Theorem) 18 minLecture22.13
-
Numerical problem ( Baye’s Theorem) 10 minLecture22.14
-
Mean and Variance of a random variable 09 minLecture22.15
-
Mean and Variance of a random variable 09 minLecture22.16
-
Mean and Variance of a random variable 08 minLecture22.17
-
Mean and Variance of a discrete random variable 07 minLecture22.18
-
Numerical problem 18 minLecture22.19
-
Bernoulli’s Trials & Binomial Distribution 11 minLecture22.20
-
Numerical problem 12 minLecture22.21
-
Mean and Variance of Binomial Distribution 05 minLecture22.22
-
Chapter Notes – ProbabilityLecture22.23
-
-
23.Limits
4-
Introduction to limits 35 minLecture23.1
-
Numerical problems 27 minLecture23.2
-
Rationalization 33 minLecture23.3
-
Limits in trigonometry 29 minLecture23.4
-
-
24.Partial Fractions
4-
Introduction to partial fraction 27 minLecture24.1
-
Partial Fractions 02 29 minLecture24.2
-
Partial Fractions 03 17 minLecture24.3
-
Improper partial fraction 20 minLecture24.4
-
Chapter Notes – Integrals
Let f(x) be a function. Then, the collection of all its primitives is called the indefinite integral of f(x) and is denoted by ∫f(x)dx. Integration as inverse operation of differentiation. If d/dx {φ(x)) = f(x), ∫f(x)dx = φ(x) + C, where C is called the constant of integration or arbitrary
Symbols f(x) → Integrand
f(x)dx → Element of integration
∫→ Sign of integral
φ(x) → Anti-derivative or primitive or integral of function f(x)
The process of finding functions whose derivative is given, is called anti-differentiation or integration.

Geometrical Interpretation of Indefinite Integral
If d/dx {φ(x)} = f (x), then ∫f(x)dx = φ(x) + C. For different values of C, we get different functions, differing only by a constant. The graphs of these functions give us an infinite family of curves such that at the points on these curves with the same x-coordinate, the tangents are parallel as they have the same slope φ'(x) = f(x).
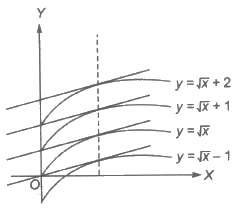
Consider the integral of 1/2√x
i.e., ∫1/2√xdx = √x + C, C ∈ R
Above figure shows some members of the family of curves given by y = + C for different C ∈ R.
Comparison between Differentiation and Integration
(i) Both differentiation and integration are linear operator on functions as
d/dx {af(x) ± bg(x)} = a d/dx{f(x) ± d/dx{g(x)} and ∫[a.f(x) ± b.g(x)dx = a ∫f(x)dx ± b ∫g(x)dx
(ii) All functions are not differentiable, similarly there are some function which are not integrable.
(iii) Integral of a function is always discussed in an interval but derivative of a function can be
(iv) Geometrically derivative of a function represents slope of the tangent to the graph of function at the point. On the other hand, integral of a function represents an infinite family of curves placed parallel to each other having parallel tangents at points of intersection of the curves with a line parallel to Y-axis.
Rules of Integration
Method of Substitution
Basic Formulae Using Method of Substitution
If the degree of the numerator of the integrand is equal to or greater than that of denominator divide the numerator by the denominator until the degree of the remainder is less than that of denominator i.e.,
(Numerator / Denominator) = Quotient + (Remainder / Denominator)
Trigonometric Identities Used for Conversion of Integrals into the Integrable Forms
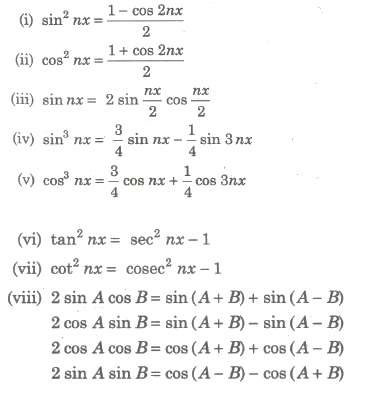
Standard Substitution

Special Integrals

Important Forms to be converted into Special Integrals
(i) Form I
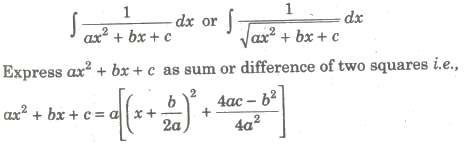
(ii) Form II
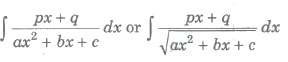
Put px + q = λd / dx (ax2 + bx + c) + mu; Now, find values of λ and mu; and integrate.
(iii) Form III
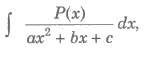
when P(x) is a polynomial of degree 2 or more carry out the dimension and express in the form P(x) / (ax2 + bx + c) = Q(x) + R(x) / (ax2 + bx + c), where R(x) is a linear expression or constant, then integral reduces to the form discussed earlier.
(iv) Form IV
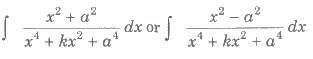
After dividing both numerator and denominator by x2, put x – a2 / x = t or x + (a2 / x) = t.
(v) Form V
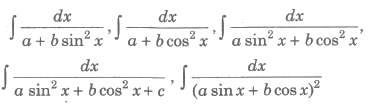
To evaluate the above type of integrals, we proceed as follow (a) Divide numerator and denominator by cos2x. (b) Rreplace sec2x, if any in denominator by 1 + tan2 x. (c) Put tan x = t, then sec2xdx = dt
(vi) Form VI
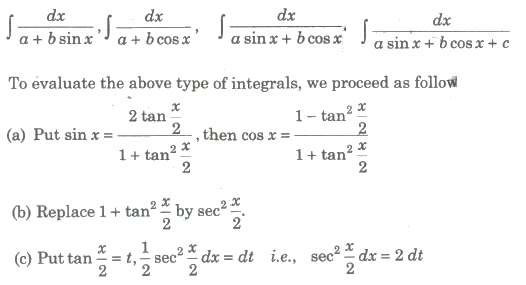
(vii) Form VII

(viii) Form VIII

(ix) Form IX
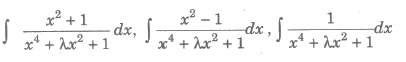
To evaluate the above type of integrals, we proceed as follows
• Divide numerator and denominator by x2
• Express the denominator of integrands in the form of (x + 1/x)2 ± k2
• Introduce (x + 1/x) or d (x – 1/x) or both in numerator.
• Put x + 1/x = t or x – 1/x = t as the case may be.
• Integral reduced to the form of ∫ 1 / x2 + a2dx or ∫ 1 / x2 + a2dx
(x) Form X
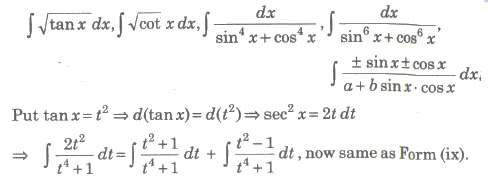
Integration by Parts
This method is used to integrate the product of two functions. If f(x) and g(x) be two integrable functions, then
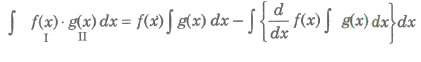
(i) We use the following preferential order for taking the first function. Inverse→ Logarithm→ Algebraic → Trigonometric→ Exponential. In short we write it HATE.
(ii) If one of the function is not directly integrable, then we take it a the first function.
(iii) If only one function is there, i.e., ∫log x dx, then 1 (unity) is taken as second function.
(iv) If both the functions are directly integrable, then the first function is chosen in such a way that its derivative vanishes easily or the function obtained in integral sign is easilY integrable.
Integral of the Form
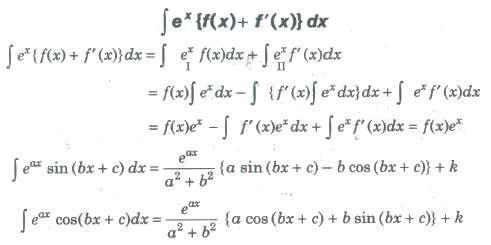
Integration Using Partial Fractions
(i) If f(x) and g(x) are two polynomials, then f(x) / g(x) defines a rational algebraic function of x. If degree of f(x) < degree of g(x), then f(x) / g(x) is called a proper rational function.
(ii) If degree of f(x) ≥ degree of g(x), then f(x) /g(x) is called an improper g(x) rational function.
(iii) If f(x) / g(x) isan improper rational function, then we divide f(x) by g(x) g(x) and convert it into a proper rational function as f(x) / g(x) = φ(x) + h(x) / g(x).
(iv) Any proper rational function f(x) / g(x) can be expressed as the sum of rational functions each having a simple factor of g(x). Each such fraction is called a partial fraction and the process of obtaining them, is called the resolution or decomposition of f(x) /g(x) partial fraction.

Shortcut for Finding Values of A, B and C etc.
Case I. When g(x) is expressible as the product of non-repeated line factors.
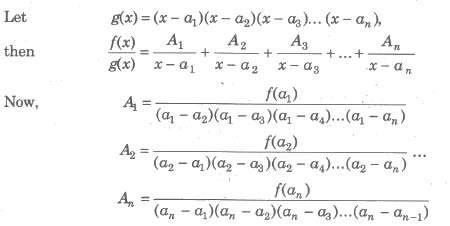
Trick To find Ap put x = a in numerator and denominator after P deleting the factor (x — ap).
Case II. When g(x) is expressible as product of repeated linear factors.
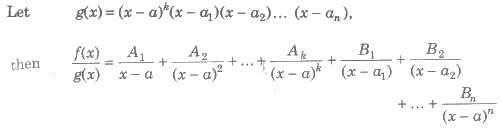
Here, all the constant cannot be calculated by using the method in Case I. However, Bl, B2, B3, … , Bn can be found using the same method i.e., shortcut can be applied only in the case of non-repeated linear factor.
Integration of Irrational Algebraic Function
Irrational function of the form of (ax + b)1/n and x can be evaluated by substitution (ax + b) = tn, thus

Integrals of the Type (bxm + bxn)P
Case I. If P ∈ N (natural number) we expand the binomial theorem and integrate.
Case II. If P ∈ Z (integers), put x = pk, where k denominator of m and n.
Case III. If (m+1)/n is an integer, we put (a + bxn) = rk, where k is th denominator of the fraction.
Integration of Hyperbolic Functions
• ∫sinh x dx = cosh x + C
• ∫cosh x dx = sinh x + C
• ∫sech2x dx = tanh x + C
• ∫cosech2x dx = – coth x + C
• ∫sech x tanh x dx = – sech x + C
• ∫cosech x coth x dx = – cosech x + C
Case IV If {(m+1)/n} + P is an integer, we put (a + bxn) = rkxn is the denominator of the fraction p.